This post is a collection of my notes on Lucas Brutschy et al’s paper “Effective Serializability for Eventual Consistency”. A later version of this paper has been accepted to POPL’17.

Introduction

Serializability is a well-understood criterion to reason about concurrent transactions. Enforcing serializability via pessimistic concurrency control techniques, such as S2PL, is very expensive. Papadimitriou shows that checking a transaction history for serializability is NP-complete, hence optimistic concurrency control methods are no good either. However, Papadimitriou also shows that it is possible to construct efficient algorithms to detect violations of stronger variants of serializability. One such well-known variant is conflict-serializability. A history is conflict-serializable iff it has no conflicts among write-read, write-write and program-order dependencies. Conflict serializability, being a syntactic check, can be implemented efficiently by algorithms that detect cycles in the dependency graphs. However, conflict-serializability is stronger than serializability in the sense that it is possible for a history to exhibit conflicts in its dependency graph, yet be observably equivalent to a serial schedule. This may happen if the conflicts are not semantically relevant. An example is the following history of three concurrent transactions (T1, T2, and T3):

w1(A), w2(A), w2(B), w1(B), w3(B)

There is a write-write dependency from T1 to T2 w.r.t A, and another write-write dependency from T2 to T1 w.r.t B. The cycle in the dependency graph means that the history is not serializable. However, considering that later writes to an object absorb the effects of earlier writes, the schedule is observationally equivalent to the following serial schedule:

w1(A), w1(B), w2(A), w2(B), w3(B)

Hence, the schedule is effectively serializable, although it is not conflict-serializable. In the context of relational databases, where reads and writes are the only atomic actions, overlooking absorption is the main reason why serializable schedules are classified as non-serializable. But as we raise the level of abstraction to more sophisticated atomic actions, e.g., add or listLength, commutativity also becomes a reason to relax the definition of conflict-serializability. The main contribution of the paper is therefore to relax the definition of conflict-serializability to account for commutativity and absorption. The paper also generalizes the definition of (relaxed) conflict serializability to be applicable for histories generated by non-SC stores. Such histories, unlike the totally ordered SC histories shown above, are only partially ordered.

Technical Development

Actions are atomic actions with possible return values, such as x.set(0), x.add(2), x.get():2 etc. Action semantics is given as prefix-closed set of legal action sequences. For example, x.set(0), x.add(2), x.get():2 is a legal action sequence. The specification of an action is a possibly-infinite set of such action sequences. Two action sequences are equivalent (≡) iff they are legal in exactly the same contexts. Thus x.set(0), y.set(1) and y.set(1), x.set(0) are equivalent because whenever the former appears in a legal action sequence, it can be replaced by the latter preserving the legality, and vice-versa. Observe that the definition of the legality is cleverly crafted to subsume the notion of observational equivalence; two legal action sequences containing the same set of actions are observationally equivalent. Thus, any transformation done on a sequence while preserving legality results in a sequence that is observationally equivalent.

Commutativity and absorption can now be specified in terms of equivalent action sequences. Two actions u and v are commutative iff uv ≡ vu. Likewise, v absorbs u iff uv ≡ v.

Since there is no need to consider order between adjacent commutative actions, we can relax such orders in an action sequence. The resultant partial order is called a trace. We furthermore divide the set of actions ($E$) into updates ($U$), for which return values are not relevant, and queries ($Q$), for which only the return values are relevant. Authors assume that updates have not preconditions whatsoever, hence any action sequence containing only the updates is legal.

Let us now consider histories. As described above, SC histories are linear action sequences. However, under weaker levels of consistency, histories are only partially ordered w.r.t $po ~\subseteq~ E \times E$, the program order, $vi ~\subseteq~ U\times Q$, the visibility order, and $ar ~\subseteq~ E \times E$, the arbitration trace. Visibility describes what updates are visible to what queries, and arbitration totally orders non-commutative actions (e.g., via timestamps). Since $ar$ is a trace, commutative actions are not directly related by arbitration, but they may be related transitively via a non-commutative action. As with an SC history, the set of actions is partitioned into multiple transactions $T$. Thus, a weakly consistent history (or schedule) is the tuple $(E,po,vi,ar,T)$ (note: we conflate the notions of history and schedule, although the paper doesn’t). For a weakly consistent schedule to be considered well-formed, it must satisfy the following properties:

1. $po ~\cup~ vi$ must be lower-finite and acyclic.
2. Let $\alpha$ be the action sequence of updates visible to a query $q$ order as per the arbitration order. Then, $\alpha q$ must be a legal action sequence.
3. The set of updates $u$ invisible to a query $q$ must be finite (the liveness requirement of eventual consistency).

As an example, consider a query q that witnesses updates {u1,u2,u3,u4,v1,v2}. Their collective arbitration trace might look like the following:

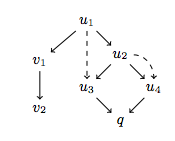
Solid arrows denote $ar$ and dotted arrows denote absorption. The two updates v1 and v2 are not dependencies of q because they do not precede it in the trace order (maybe v1 and v2 are y.set(0) and y.add(1), whereas q is x.get()), and therefore can be “moved past” q. The update u2 is not a dependency of q either as it gets absorbed by the adjacent update u4. But after that u1 and u3 become adjacent, and so u1 can get absorbed by u3. What remains are the two dependencies u3 and u4 of q.

The algorithm to find dependencies of a query q is described below with help of the above example:

1. Start with a set of all updates visible to q that directly precede q in $ar$.
   • For q in the above figure, the set is {u3,u4}
   • Updates v1 and v2 are thus already eliminated.
2. Lets call the set as $\oplus$. In each iteration, expand the boundaries of $\oplus$ by including updates that precede those in the set in the $ar$ order without being absorbed by them (i.e., related to those in the set by a solid arrow, but not a dashed arrow). If an update (u) is absorbed by another update in the set, remove u, and relate all updates that precede u (in $ar$) to all updates that succeed u.
   • For the current example, the only update preceding the elements in the set $\oplus$ = {u3,u4} is u2. However, u2 is absorbed by u4, so we remove it from the trace and relate u1 to both u3 and u4.
   • In the next iteration, u1 precedes the elements in $\oplus$, but it is absorbed by u3 in $\oplus$, hence it too must be removed.
3. We iterate until there are no more updates left to be included in $\oplus$.
   • The final $\oplus$ for the current example is thus {u3,u4}.

The set $\oplus$ is the dependency set of q, and contains all the updates that must be ordered before q in any serialization of the original weakly consistent schedule. It is informative to note that if we do not take commutativity and absorption into account, the dependency set would have been equal to the visibility set of q.

The notion of dependency has a natural counterpart called anti-dependency. An anti-dependency of a query in a given schedule is an update not visible to the query but such that making it visible would turn it into a dependency.

Thus, the set $\ominus$, the anti-dependency set of q, contains all the updates that must be ordered after q in any serialization of the original weakly consistent schedule. Computing the set $\ominus$ of q is simple: find an update u not visible to q in the original schedule, and make it visible. Now, run the above algorithm to compute $\oplus$ set of q. If $\oplus$ contains u, the u is an anti-dependency of q, otherwise not. Again, it is informative to note that if we do not consider commutativity and absorption, all updates not visible to q are its anti-dependencies.

Once we compute $\oplus$ and $\ominus$ for all the queries, a serial order can be obtained by topologically ordering the graph $po ~\cup~ ar ~\cup~ \oplus ~\cup~ \ominus$. If the graph contains a cycle, then we have a conflict, and the schedule is not serializable.

Evaluation

The evaluation is notable for its breadth. 33 TouchDevelop applications have been analyzed. TouchDevelop uses global sequence protocol (gsp) to implement a replication system with prefix consistency (stronger than causal). Nonetheless, even if the store is SC, serializability violations are possible because of dependency violations among transactions (groups of atomic actions). As our experience with RDBMS tranasactions informs, serializability violations are abound under weak isolation, and requiring serializability for all transactions is a giant overkill. As a thumb rule, authors assume that SER violations involving query transactions (transactions issued by the display code) as harmless, hence exclude them from the evaluation. Among the remaining transactions, many SER violations have been found. Some examples discussed in the paper:

1. Tetris code where high-score is being locally updated (mutable integer). This is obviously incorrect. Fix is to basically turn the high score integer into an op-based data structure.
2. Event management code where the app sorts the cloud-backed list of events by removing the events, sorting them locally, and re-inserting them. Fix is to either do it in a SER transaction, or to simply stop doing that. Sort locally whenever event list is being queried.
3. A quiz game that allows a user to overwrite an existing user account due to incorrect uniqueness check. Fix is to use CAS.
4. A Tic-Tac-Toe game that uses mutable datatypes all over. The fix is to use a data model that is op-based.

Another round of evaluation is done with TPC-C implementation on top of Riak (an EC store with no strengthening). Some violations:

1. A DELIVERY transaction that updates a mutable balance. Obviously, one of the updates is lost when two DELIVERY transactions run concurrently. The fix is to use a CRDT counter for balance.
2. DELIVERY transaction also has a subsequent getBalance operation, so even if the balance is a CRDT, SER violations still exist. However, this violation is ignored since it is harmless.
3. The percieved foreign-key violation between ORDERS and NEW_ORDERS tables manifests as an SER violation. The fix proposed is denormalization of data, although enforcing monotonic reads via QUORUM writes would fix the issue.
4. Two NEW_ORDER transactions assign same id to a transaction. The behaviour is not serializable, and the only fix is to use CAS.

Observations and Questions

1. It is remarkable that testing could uncover uniqueness bugs and foreign key bugs since they require concurrent transactions to issue operations on very specific keys and ids (uniqueness for example requires to randomly issued NEW_ORDER transactions to insert an order with exact same id See comments).
2. Moreover, uncovering these bugs requires conflicting transactions to overlap in a specific manner. Such concurrent schedules are hard to trigger, aren’t they?
3. This leads to the question: what is the test harness and testing methodology?
4. Perceived foreign key violation has been uncovered by analyzing a query transaction. It is for this reason that I don’t feel comfortable excluding query transactions.
5. With mutable data, lost updates are inevitable. That is, the presence of UPDATE ... SET queries in weakly isolated transactions is itself a sufficient condition to witness SER violations. 4 of the 8 bugs discussed above fall into this category. The fix proposed in all the cases is to basically turn the mutable data into an op-based RDT. Assuming that we start we such an implementation, how many new bugs would be uncovered? What are the fixes?
6. It would be interesting to apply effective serializability criterion to replicated versions of stacks and queues. Experience tells us that replicating these data structures in a coordination-free fashion is quite tricky.