Today, in our reading group, we read an interesting paper titled “Disciplined Inconsistency” by Brandon Holt et al from UW CSE. This post is my notes on the paper.

Background

Modern day web-services often trade consistency for availability and performance. However, there exist some data and operations for which stronger forms of consistency are needed. Recognizing this, some data stores, including Quelea, implement stronger consistency guarantees, such as Causal Consistency. However, there are two major problems with the lattice-of-consistency-levels model espoused by Quelea:

• In real applications, invariants over the data are almost never strict. Applications can tolerate certain amount of error, especially if it improves the performance. For example, Amazon can afford to oversell a discounted item by 2% of the available stock, but no more. Unfortunately, Quelea’s model is insensitive to such error bounds. Quelea expects applications to have exact invariants, such as non-negative balance or monotonicity, and attempts to statically determine appropriate consistency levels that can enforce these invariants without fail. In reality, applications execute under moderate-to-medium loads during most of their lifetimes, under which weaker consistency levels are more-or-less sufficient to maintain application invariants. Quelea’s consistency model lacks dynamic monitoring, thus cannot adapt consistency to the changing load conditions.
• The flow of data between operations executing at various consistency levels is not controlled. Consequently, data being maintained at EC can make its way into the data being maintained at SC.

Holt et al propose a system called IPA (Inconsistent, Performance-bound, Approximate storage system) that addresses the above problems via a combination of static type system and runtime enforcement. In the following, I explain various aspects of IPA in greater detail.

IPA’s Programming Model

IPA is modeled as a data structure store, like Redis, Riak, and Hyperdex, and its Scala-based programming framework allows programmers to implement ADTs, such as sets and counters, as distributed data structures. To better understand IPA’s approach, let us distinguish between library writers, who implement ADTs, and app developers, who use ADTs. IPA expects library writers to define various versions of an ADT, each with a different combination of consistency policies for ADT operations. In Scala’s terminology, each combination is a trait of the ADT. For instance, Counter ADT can be defined with, say, two traits: a WeakOps trait that implements counter reads and increments using Cassandra’s weak (i.e., consistency level ONE) reads and writes, and a StrongOps trait that implements them via Cassandra’s QUORUM reads and writes, or via ONE writes and ALL reads. For more sophisticated ADTs, more combinations of consistency levels for operations can be implemented as traits. App developers use the ADTs defined by library writers by selecting a version with desired trait. For instance, an app developer may use the Counter ADT with StrongOps trait to obtain a strongly consistent counter, or with WeakOps to obtain a weakly consistent counter.

From IPA’s perspective, Strong and Weak are examples of static consistency policies. IPA also provides support for library writers to implement traits for dynamic consistency policies, such as LatencyBound and ErrorBound, which admit bounds on the latency of an operation and the error tolerance on its result (resp.). For instance, LatencyBound trait for Counter ADT can be implemented using the rush primitive offered by IPA that executes a read or a write under strongest consistency level possible within the specified time limit. Likewise, ErrorBound trait can be implemented via IPA’s support for escrow reservations. Both these mechanisms will be explained in detail later. An app developer, however, does not need to know about these implementation mechanisms. The developer can choose Counter with LatencyBound(50) trait to obtain a counter whose operations have a 50ms latency bound, or Counter with ErrorBound(10) trait to obtain a counter whose value can be off by at most 10% of the actual count.

IPA thus exposes different levels of abstractions to library writers and app developers. While app developers can think in terms of ADTs and high-level consistency policies, library writers have to face the ugliness of the underlying data store as they reason in terms of reads, writes, and low-level consistency policies, such as ONE, QUORUM etc. While IPA does provide some tool support (via rush and reservations), it does not raise the level of abstraction insofar as library writers are concerned. This is in contrast to Quelea where RDT writers also reason in terms of high-level consistency policies and RDT-specific effects.

Static Type System

The stated purpose of IPA’s consistency type system is to enforce consistency safety Informally, it “ensures that values from weakly consistent operations cannot flow into stronger consistency operations without explicit endorsement form the programmer”. Thus, the type system helps developers trade consistency for performance in a disciplined manner.

IPA’s implementation defines four consistency types:

• Consistent[T]: A value of type T resulting from a strongly consistent operation (the StrongOps trait),
• Inconsistent[T]: A value of type T resulting from a weakly consistent operation (the WeakOps trait),
• Rushed[T]: A value of type T resulting from an operation executed with a latency bound (the LatencyBound trait), and
• Interval[T]: A range of values of type T, each of which is equally likely to be the result of an operation executed with an error bound (the ErrorBound trait).

The return type of an ADT operation is either defined by the library writer while implementing the trait, or follows from the use of IPA primitives, such as rush. Thus, more consistency types can be defined by library writers. For example, consider a Facebook-like deployment where an object is only ever stored in a single data center. If an ADT is tailor-made for such deployment, its writer can implement its operations via LOCAL_QUORUM reads and writes, and claim per-object sequential consistency by annotating the return types of operations with a new Consistent[PoSC] type.

A subtype lattice over consistency types can also be defined by relying on Scala’s type system. For instance, here is a lattice defined by the IPA implementation, and presented in the paper:

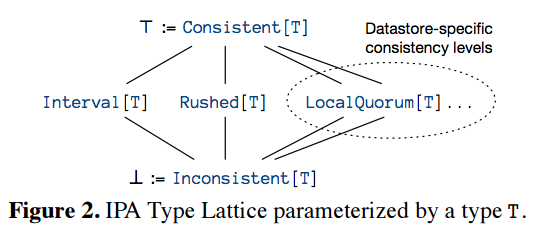
The result of annotating return values with consistent types is that app developers must now explicitly handle non-Consistent[T] values:

• If a value is Inconsistent[T], the developer must explicitly endorse the value for it to be treated on par with Consistent[T] values.
• If it is Interval[T], the result of an ErrorBound operation, then the developer has to handle an interval of values.
• Rushed[T] is implemented as “a sum type with one variant per consistency level available to the implementation of LatencyBound” (It’s not quite clear to me how this is done). Thus, a Rushed[T] value has to be destructed and matched against Consistent[T], or Inconsistent[T], or any other user-defined (static) consistency type before it is used.

Thus consistency types let application be sensitive to the consistency level of a value. Alternatively, they force the application to adopt a disciplined approach while dealing with inconsistent values.

Run-time enforcement of consistency

Strong consistency is implemented using QUORUM reads and writes. As we describe in Representation without Taxation paper, such an implementation is likely to be buggy since Cassandra’s LWW conflict resolution drops writes due to inevitable clock drift across servers.

LatencyBound reads are implemented in IPA by issuing parallel read requests at different (Cassandra) consistency levels, and returning the strongest available result at the specified time limit. One drawback with this approach is that it floods network with read requests, which is undesirable esp. when system is operating at high loads. Therefore, the paper proposes an alternative approach that is based on monitoring latency. The approach first computes the likely latency (e.g., 90th percentile latency) of a read operation for each consistency level based on the recent history, and then issues the read at an appropriate level. For this purpose, the system monitors latencies of reads, grouped by operation and consistency level. “The monitor uses an exponentially decaying reservoir to compute running percentiles weighted toward recent measurements, ensuring that its predictions continually adjust to current conditions”.

IPA allows ADTs to implement error bounds making use escrow and reservation. The paper summarizes this concept well:

The idea is to set aside a pool of permissions to perform certain update operations (we’ll call them reservations or tokens), essentially treating operations as a manageable resource. If we have a counter that should never go below zero, there could be a number of decrement tokens equal to the current value of the counter. When a client wishes to decrement, it must first acquire sufficient tokens before performing the update operation, whereas increments produce new tokens. The insight is that the coordination needed to ensure that there are never too many tokens can be done off the critical path: tokens can be produced lazily if there are enough around already, and most importantly for this work, they can be distributed among replicas. This means that replicas can perform some update operations safely without coordinating with any other replicas.

Consider an increment-only counter X. Let us say X = 100 initially, and the error bound on X is 10%. Consider a case when 3 replicas are independently modifying X. Then, replicas can be issued 5 tokens each, capturing the fact that each can perform 5 increments before they need to synchronize in order to not violate error bounds. For instance, if all replicas perform 5 increments each without synchronizing, then each will return 105 as the value of X when the actual value is 115. However, 105 is still within 10% of 115, so this is alright. Thus, error bounds provide applications with some slack in implementing strongly consistent operations by allowing synchronization to be moved off the critical path.

IPA provides infrastructure support (via reservations server) for escrow reservations, and exposes its functionality via an API. The library writer is expected to make use of this functionality to implement ErrorBound consistency policy for his/her ADT.

An Aside

The escrow method was proposed in 1986 (and rehashed later), but there seem to be many recent papers on applying variants of escrow in various contexts:

• Liu et al, Warranties for Faster Strong Consistency, NSDI’14 (paper).
• Balegas et al, Putting Consistency Back into Eventual Consistency, EuroSys’15 (paper)
• Balegas et al, Extending Eventually Consistent Cloud Databases for Enforcing Numeric Invariants, SRDS’15 (paper)

I have the intuition that escrow methods would be useful to implement merge operation on data structures that support non-commutative and non-idempotent operations. Basically, if we allocate n tokens to each replica to perform a non-idempotent operation, such as a dequeue operation on a queue, n times (where n is the size of the queue), then merge operation becomes simple because a dequeue only dequeues an item present on all replicas. We also get the read at least once guarantee on the messages in the queue.

Experiments

The experimental methodology of the paper is interesting, and results are insightful. Experiments are performed for two different setups: simulation and real. In simulation experiments, they use multiple docker containers on the same physical node connected via the Ethernet to simulate multiple replicas. Network conditions are controlled via Linux’s tc netmem utility that introduces packet delay and loss at the OS level. In real experiments, they deploy IPA on Google’s Compute Engine with geo-distributed replicas.

Three kinds of experiments were performed: 1. With uniform 5ms network latency between replicas (simulating a local network in a data center under medium-to-high load), 2. With one replica being slower than other replicas (modeling variable network latency and hardware problems), and 3. With real geo-distributed replicas. Some highlights:

• In experiments with a single slow replica, 50ms bound on the 95th percentile latency overloads the slow replica with double the requests (why?), and causes it to exceed the latency bound 5% of times.
• In geo-distributed case, if all operations are SC, then the mean latency is 800ms, but if 1% error is tolerated (on the Counter), then the latency reduces significantly to 200ms. The latency difference between weak consistency policy and 5% ErrorBound consistency policy is negligible. This experiment demonstrates that it is possible to guarantee error bounds on the data without having to forego availability and performance.