Git’s merge algorithm seems to have inexplicable semantics leading to some interesting cases. I describe a couple of examples below. The bottom line is that:
- Git merge is inconsistent: Merge result seems to depend not just on what versions were merged, but also how they were merged. Thus two branches that pulled the same set of user commits may end up with different versions.
- Git merge is unintuitive: The result of a successful (auto) merge may not necessarily be what we expect.
Note that I distinguish between user commits and merge commits in this post. Assuming that all merges are automerges (i.e., there are no merge conflicts), I expect two branches with same history of user commits to be consistent, i.e., have the same final version.
Example 1
This example shows that Git automerging leads to inconsistent results. Thus if you and your colleague are working on parallel branches with exact same set of user commits, your code may still have vulnerabilities and bugs that your colleague’s code doesn’t. So you have to independently review your code notwithstanding your colleague’s assurances.
To demonstrate this point, let’s start with a file foo.js containing
Javascript/JQuery pseudo-code:
/*some computation on data happens here */
$.ajax({
type: "POST",
url: url,
data: encrypt(data),
success: function(response) {
$(".result").html(response);
}),
dataType: "text"
});Let’s commit it to master:
git init; git add foo.js; git commit -m "foo.js added"
Now fork two branches, temp1 and temp2, from master:
git checkout -b temp1; git checkout master
git checkout -b temp2; git checkout master
With three branches in place, let us manifest the version control
graph shown in the below figure. Vertices in the graph are distinct
versions. The diff of each version w.r.t its parent is highlighted.
Edges leading to a version are labeled with the Git actions that led
to the version. In case of a git commit, only the commit message is
shown (in quotes). The actions are numbered, and each action is
explained in greater detail below the figure. Each of the three
branches is assigned a different color background.
Now take a look at the version graph, and follow the explanation below the figure to understand it.
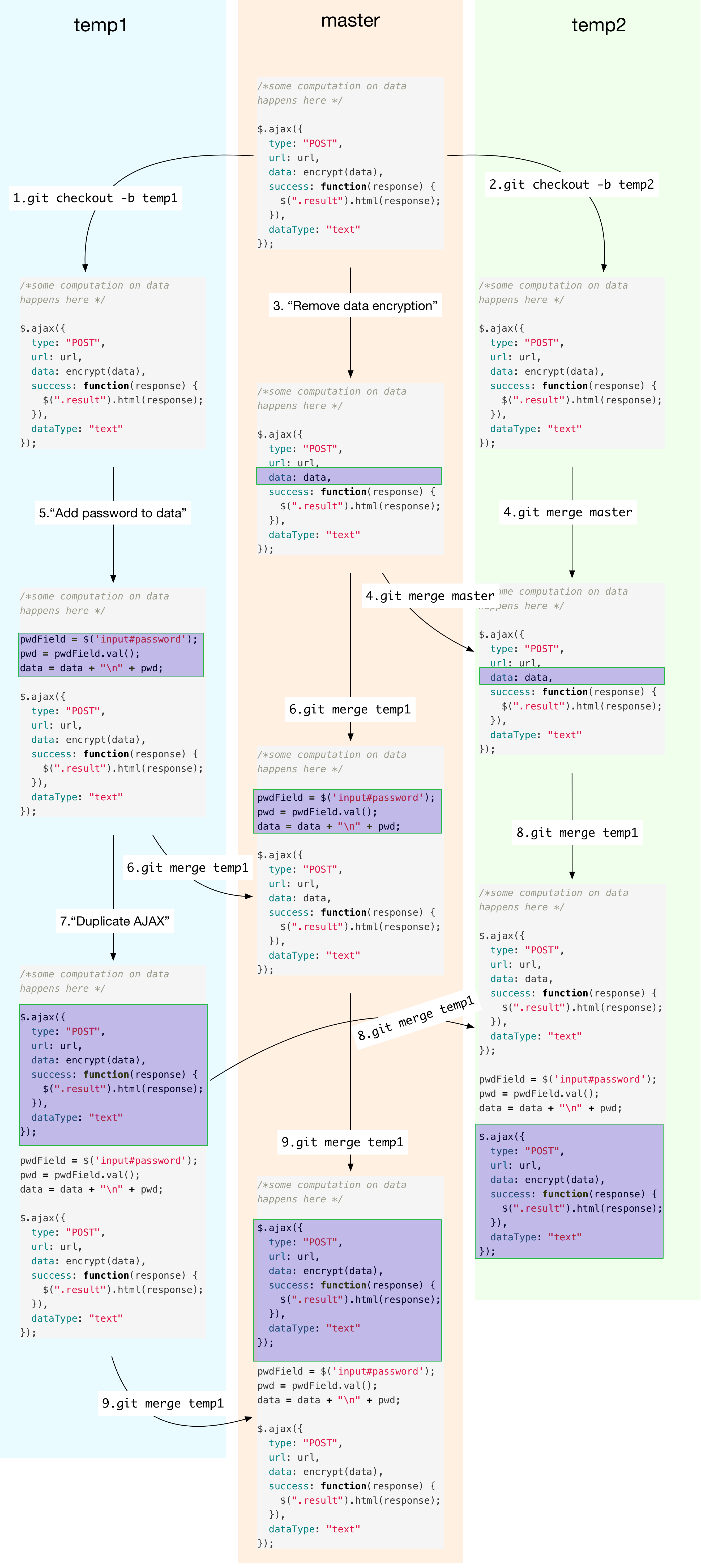
Actions 1 and 2 fork branches temp1 and temp2 as described
previously. Actions 3-9 do the following:
- Action 3: On the master branch, we might decide to remove encryption
as
datacontains nothing sensitive. - Action 4: Your colleague Alice starts development on
temp2by fast-forwarding it to current master (your latest version). - Action 5: Independently on
temp1branch, your other colleague Bob decides to add sensitive information (password) todatasince it is anyway sent encrypted. - Action 6: You pull the latest changes from Bob. Git automerges, and says everything is fine. You don’t do anything.
- Action 7: On
temp1, Bob may decide to commit a version that sends the data twice, for whatever reason. - Action 8: Alice pulls Bob’s latest version from
temp1ontotemp2. She decides to review the code and sees two AJAX POSTS - first without data encryption and second with encryption. Since password is only sent the second time, she finds nothing wrong with the code, hence signs it off. - Action 9: Now you pull Bob’s latest version from
temp1. You want to review the code, but learn that Alice has already signed off her code ontemp2which has the same history of user commits as yours (see below). Relying on Alice’s judgment, you sign off your code and deploy in production. - Your code now sends passwords unencrypted although Alice’s doesn’t.
You can see the this example on Github
with few minor changes: I used branch main instead of master, and
sha256 instead of encrypt.
The final commit histories of main and temp2 are shown below.
Observe that both branches have same set of user-generated commits
(3e3256, 31001b, 73a645, and 8004f4). The merge commits are
all result of Git’s automerge.
$git branch
main
master
temp1
* temp2
$git log
commit 291329350e5ede0163ebdf9cb31ab0ad207ebb18 (HEAD -> temp2)
Merge: 31001b0 8004f40
Author: GitUser <gituser@example.com>
Date: Mon Nov 25 07:25:45 2019 -0500
Merge branch 'temp1' into temp2
commit 8004f40b718538d53458f2218b52f81c8c7e43a1 (temp1)
Author: GitUser <gituser@example.com>
Date: Sun Nov 24 20:06:16 2019 -0500
two ajaxes now
commit 73a645e9803b74dd9eac212ec706eb01fa328c5e
Author: GitUser <gituser@example.com>
Date: Sun Nov 24 20:03:01 2019 -0500
pwd added
commit 31001b08380cad566d83b14ec1adecbb2836e399
Author: GitUser <gituser@example.com>
Date: Sun Nov 24 19:52:49 2019 -0500
removed sha256
commit 3e325647d435895b8b1f526fbde9bd9208a555e7 (master)
Author: GitUser <gituser@example.com>
Date: Sun Nov 24 19:50:52 2019 -0500
adding foo.js
$git checkout main
Switched to branch 'main'
$git log
commit a52b2517b747d7804fe02ae5bb7425ea57b5908f (HEAD -> main)
Merge: b2c3403 8004f40
Author: GitUser <gituser@example.com>
Date: Sun Nov 24 20:06:29 2019 -0500
Merge branch 'temp1' into main
commit 8004f40b718538d53458f2218b52f81c8c7e43a1 (temp1)
Author: GitUser <gituser@example.com>
Date: Sun Nov 24 20:06:16 2019 -0500
two ajaxes now
commit b2c3403b4254bc01553871d06526c438c53f3952
Merge: 31001b0 73a645e
Author: GitUser <gituser@example.com>
Date: Sun Nov 24 20:03:23 2019 -0500
Merge branch 'temp1' into main
commit 73a645e9803b74dd9eac212ec706eb01fa328c5e
Author: GitUser <gituser@example.com>
Date: Sun Nov 24 20:03:01 2019 -0500
pwd added
commit 31001b08380cad566d83b14ec1adecbb2836e399
Author: GitUser <gituser@example.com>
Date: Sun Nov 24 19:52:49 2019 -0500
removed sha256
commit 3e325647d435895b8b1f526fbde9bd9208a555e7 (master)
Author: GitUser <gituser@example.com>
Date: Sun Nov 24 19:50:52 2019 -0500
adding foo.js
Example 2
In the previous example, branches main and temp2 obtained the same
set of user commits, but with different number of pulls/merges.
main pulled from temp1 in two steps – first merging the
intermediate version, and then merging the final version, whereas
temp2 pulled only once – the final version. The inconsistency shows
that the granularity of merges matter. I will now describe another
example, which demonstrates that the merge result also depends on the
order of merging branches. That is, two branches pull the same set
of user commits, but still end up with different versions because they
pull the commits in different orders. The example also involves a
scenario where automerge succeeds, but result doesn’t agree with our
intuition.
Similar to the previous example, let’s start with a file foo.js
containing Javascript/JQuery pseudo-code:
/*some computation on data */
$.ajax({
type: "POST",
data: encrypt(data),
url: url,
success: function(response) {
$(".result").html(response);
}),
dataType: "text"
});Let’s commit it to master:
git init; git add foo.js; git commit -m "foo.js added"
Fork four branches, a, b, c, and d:
git checkout -b a; git checkout master
git checkout -b b; git checkout master
git checkout -b c; git checkout master
git checkout -b d; git checkout master
On each of the four branches, we make distinct changes to foo.js and
commit. The four new commits are visualized in the figure below.
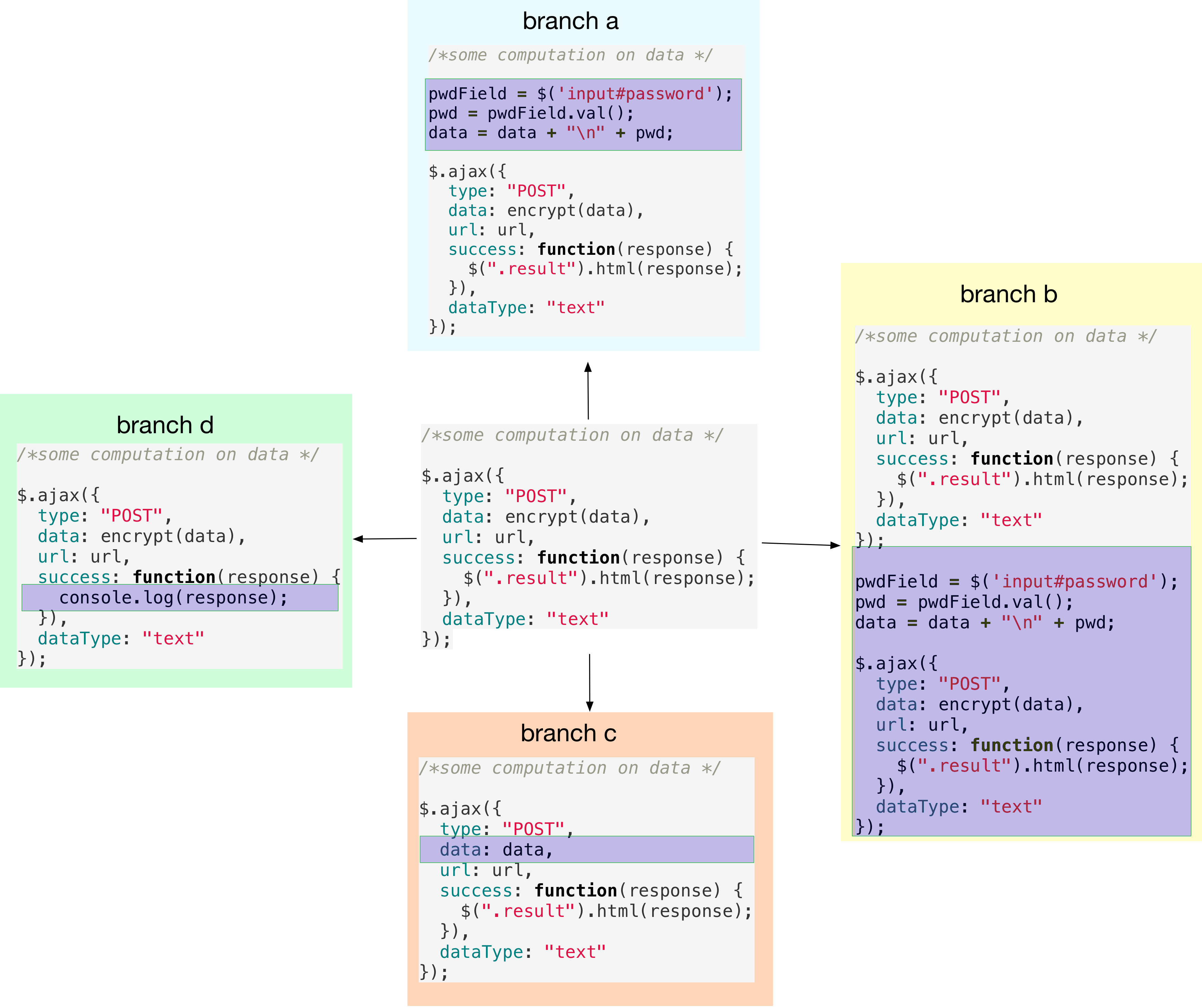
Let us now fork one more branch, temp, from master:
git checkout master; git checkout -b temp
We will now merge branches a, b, c, and d into master and
temp in different orders and show that the resultant versions are
different.
- On master, the merge order is
a → c → b → d - On
temp, the merge order isd → c → b → a
Merges on master branch are visualized in the following figure. Each labeled edge represents a merge from the corresponding branch (branch heads are shown in the previous figure). As usual, the diff of each version w.r.t its previous version is highlighted.

As an aside, consider the merge from branch b. I would have expected
the merge result to be a sequence of encrypted AJAX, followed by
data + pwd logic, and finally unencrypted AJAX. A merge conflict
would have been fine too! But the actual result has data + pwd
logic twice interspersed by AJAX calls with unencrypted and encrypted
data (resp.). This is puzzling.
Let us now focus on the temp branch. The merges on temp are
visualized below:

Here again, the result of last merge (from a) is not what I
expected. Given that the contents of a are contained inside the
the merging temp version in the same order, I expected the merge to
be the same as the previous version on temp. The actual result
replicates data + pwd logic twice, and I don’t understand why.
Leaving aside the concerns of intuitiveness, one can clearly see that
that master and temp have different head versions even as both
pulled the exact same versions albeit in different order. This shows
that order in which merges are done does matter, which is a bit
disconcerting.
This example too is available on Github with minor variations.
Conclusion
The examples above demonstrate that Git merge could lead to inconsistent and unintuitive results. People who understand Git’s merge algorithm can perhaps foresee such behaviors and work their way around them, however that’s not a satisfactory justification for a well-designed system must have predictable behavior based on its interface, not its internals.
PS: If you know a definitive and concise description of Git’s merge algorithm, I’d be grateful if you can drop me a note here in comments or on twitter
Continue reading